[BOJ] 6549: 히스토그램에서 가장 큰 직사각형 (C/C++)
문제 6549번: 히스토그램에서 가장 큰 직사각형
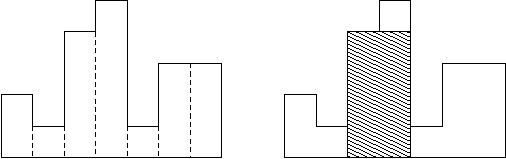
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.
히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 \(h_1, ..., h_n (0 ≤ h_i ≤ 1,000,000,000)\)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
각 테스트 케이스에 대해서, 북서풍을 타고 항해할 수 있는 섬의 쌍의 수를 출력한다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
문제분석
문제 요구사항
- 히스토그램에서 가장 큰 직사각형을 찾아야 한다. -> 만들어 지는 모든 직사각형을 탐색 하고 그중 가장 큰 직사각형의 넓이를 저장한다.
Stack을 활용하여 모든 직사각형의 넓이를 탐색한다.
구현
Pair를 넣는 Stack을 선언 한 후, Pair.first에는 n번째 직사각형의 높이를 저장하고, Pair.second에는 n을 저장시킨다. 이때 Stack의 top에 저장된 data의 직사각형의 높이가 현재 직사각형 높이보다 크다면, stack의 직사각형의 높이*(현재 index- stack.top.second)와 ans의 크기를 비교한 후 pop을 한다.
pop을 다 끝낸 후, Stack의 Top의 직사각형의 높이가 현재 높이보다 낮다면 stack에 현재 직사각형의 data를 push한다.
증명
Stack의 입장에서 생각해 보자, 먼저 Stack.top.first > 현재 직사각형의 높이라면, Stack.top의 높이를 가지는 직사각형은 현재 직사각형에 막혀 쓸모없는 데이터가 된다. 따라서 pop을 한다.
Stack.top.first == 현재 직사각형의 높이라면, Stack에 현재 직사각형의 data를 넣으면 오히려 계산되는 가로 길이를 줄이는 효과가 나타나기에 Stack에 넣지않는다.
Stack.top.fisrt < 현재 직사각형의 높이, 라면 Stack에 있는 모든 데이터의 직사각형 높이가 현재 직사각형의 높이보다 낮기 때문에, 현재 직사각형이 Stack의 데이터들을 방해하지 않게 된다. 그리고 현재 Stack에 Data를 넣으며, 현재 직사각형을 계산 범위에 넣어준다.
이러한 과정을 반복하면, 모든 직사각형에 대하여, 해당 직사각형의 높이가 가질 수 있는 최대 넓이를 계산 할 수 있음으로, 유효한 알고리즘이다.
여담
Stack을 활용한 풀이 뿐만 아닌 DP를 활용한 코드도 같이 게재 하였다.
코드
Stack
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <stack>
#include <vector>
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
while (true) {
int n;
std::cin >> n;
if (n == 0) {
break;
}
long long ans = 0;
// first is height, second is left index
std::stack<std::pair<int, int>> stk;
for (int i = 0; i < n; ++i) {
int height;
std::cin >> height;
std::pair<int, int> temp(height, i);
while (!stk.empty() && stk.top().first > temp.first) {
ans = std::max(ans, static_cast<long long>(i - stk.top().second) *
stk.top().first);
temp.second = stk.top().second;
stk.pop();
}
if (!stk.empty() && stk.top().first == temp.first) {
continue;
}
stk.push(temp);
}
while (!stk.empty()) {
ans = std::max(
ans, static_cast<long long>(n - stk.top().second) * stk.top().first);
stk.pop();
}
std::cout << ans << "\n";
}
return 0;
}
DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <stack>
#include <vector>
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
while (true) {
int n;
std::cin >> n;
if (n == 0) {
break;
}
std::vector<int> heights(n);
for (int i = 0; i < heights.size(); ++i) {
std::cin >> heights[i];
}
std::vector<std::pair<int, int>> range(n);
for (int i = 0; i < range.size(); ++i) {
range[i] = {i, i};
}
long long ans = 0;
for (int i = 0; i < range.size(); ++i) {
if (heights[i] == 0) {
continue;
}
while (range[i].first - 1 >= 0 &&
heights[i] <= heights[range[i].first - 1]) {
range[i].first = range[range[i].first - 1].first;
}
}
for (int i = range.size() - 1; i >= 0; --i) {
while (range[i].second + 1 < heights.size() &&
heights[i] <= heights[range[i].second + 1]) {
range[i].second = range[range[i].second + 1].second;
}
ans = std::max(
ans, static_cast<long long>(range[i].second - range[i].first + 1) *
heights[i]);
}
std::cout << ans << "\n";
}
return 0;
}