[BOJ] 1799: 비숍 (C/C++)

문제 1799번: 비숍

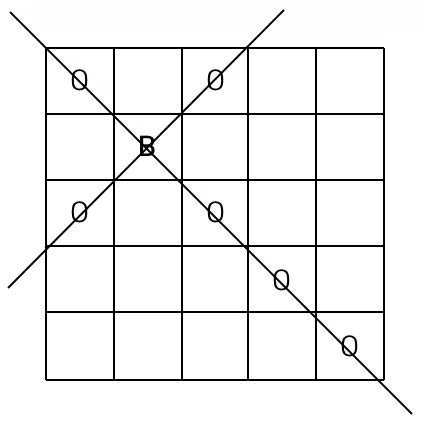
서양 장기인 체스에는 대각선 방향으로 움직일 수 있는 비숍(bishop)이 있다. < 그림 1 >과 같은 정사각형 체스판 위에 B라고 표시된 곳에 비숍이 있을 때 비숍은 대각선 방향으로 움직여 O로 표시된 칸에 있는 다른 말을 잡을 수 있다.

< 그림 1 >

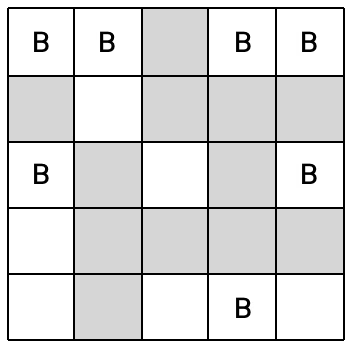
그런데 체스판 위에는 비숍이 놓일 수 없는 곳이 있다. < 그림 2 >에서 체스판에 색칠된 부분은 비숍이 놓일 수 없다고 하자. 이와 같은 체스판에 서로가 서로를 잡을 수 없도록 하면서 비숍을 놓는다면 < 그림 3 >과 같이 최대 7개의 비숍을 놓을 수 있다. 색칠된 부분에는 비숍이 놓일 수 없지만 지나갈 수는 있다.

< 그림 2 >

< 그림 3 >

정사각형 체스판의 한 변에 놓인 칸의 개수를 체스판의 크기라고 한다. 체스판의 크기와 체스판 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 주어질 때, 서로가 서로를 잡을 수 없는 위치에 놓을 수 있는 비숍의 최대 개수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다. 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로 한 줄씩 주어진다. 비숍을 놓을 수 있는 곳에는 1, 비숍을 놓을 수 없는 곳에는 0이 빈칸을 사이에 두고 주어진다.

출력

첫째 줄에 주어진 체스판 위에 놓을 수 있는 비숍의 최대 개수를 출력한다.

문제분석

문제 요구사항

• 각각의 비숍이 서로 대각선 상에 놓이지 않아야함

비숍은 대각선 상으로 움직임으로 해당 대각선에 비숍이 놓일수 있는지에 대하여 저장 한 후, 해당 데이터를 기반으로 비숍을 놓는다.

구현

전형적인 8Queen 문제이다. 하지만 비숍의 특성상 검은색 체스판에 놓인 비숍과 하얀색 체스판에 놓인 비숍끼리는 서로 영향을 미치지 못하기에, 해당 두 경우에 대하여 8Queen 문제와 같은 알고리즘으로 계산하여 준다.

증명

검은색 체스판 위에 비숍과 하얀색 체스판 위의 비숍은 서로 Disjoint하기에 각각의 경우를 8Queen 문제 알고리즘을 적용하여 풀이한다.

코드

#include <iostream>
#include <utility>
#include <vector>
int n;
std::vector<bool> diagonal_1;
std::vector<bool> diagonal_2;
std::vector<std::vector<std::pair<int, int>>> positions(2);

const int ConvertToDiagonal1(const int i, const int j) { return i + j; }

const int ConvertToDiagonal2(const int i, const int j) { return n - 1 - i + j; }

const int FindMaximumBishop(
    std::vector<std::pair<int, int>>::iterator iter,
    const std::vector<std::pair<int, int>>::const_iterator& iter_end,
    const int cnt_bishop = 0) {
  if (iter_end == iter) {
    return cnt_bishop;
  }

  int ans = 0;

  if (diagonal_1[iter->first] && diagonal_2[iter->second]) {
    diagonal_1[iter->first] = diagonal_2[iter->second] = false;
    ans = FindMaximumBishop(iter + 1, iter_end, cnt_bishop + 1);
    diagonal_1[iter->first] = diagonal_2[iter->second] = true;
  }

  return std::max(ans, FindMaximumBishop(iter + 1, iter_end, cnt_bishop));
}
int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(nullptr), std::cout.tie(nullptr);

  std::cin >> n;

  int input;
  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
      std::cin >> input;

      if (input) {
        positions[(i + j) & 1].push_back(std::pair<int, int>(
            ConvertToDiagonal1(i, j), ConvertToDiagonal2(i, j)));
      }
    }
  }

  diagonal_1.assign(2 * n - 1, true);
  diagonal_2.assign(2 * n - 1, true);

  std::cout << FindMaximumBishop(positions.front().begin(),
                                 positions.front().end()) +
                   FindMaximumBishop(positions.back().begin(),
                                     positions.back().end());

  return 0;
}