[Algorithm] CCW(Counter Clock Wise)

위키피디아의 Cross product글과 MS의 3-D Coordinate Systems를 참고하여 작성하였습니다.

CCW(Counter Clock Wise)

CCW, 즉 Counter Clock Wise 알고리즘은 외적(Cross Product)의 원리를 이용하여, 임의의 3점이 이루는 방향을 판단 하는 알고리즘 이다.

원리

위키피디아의 Cross Product글에서 Applications중 Computational geometry의 일부분을 발췌해 왔다.

In computational geometry of the plane, the cross product is used to determine the sign of the acute angle defined by three points \(\boldsymbol {p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})}\) and \(\boldsymbol {p_{3}=(x_{3},y_{3})}\). It corresponds to the direction (upward or downward) of the cross product of the two coplanar vectors defined by the two pairs of points \((p_{1},p_{2})\) and \((p_{1},p_{3})\). The sign of the acute angle is the sign of the expression

\[P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),\]

which is the signed length of the cross product of the two vectors. To use the cross product, simply extend the 2D vectors \(p_{1},p_{2},p_{3}\) to co-planar 3D vectors by setting \(z_{k}=0\) for each of them.

In the “right-handed” coordinate system, if the result is 0, the points are collinear; if it is positive, the three points constitute a positive angle of rotation around \(\boldsymbol {p_{1}}\) from \(\boldsymbol{p_{2}}\) to \(\boldsymbol{p_{3}}\), otherwise a negative angle. From another point of view, the sign of \(P\) tells whether \(p_{3}\) lies to the left or to the right of line \(p_{1},p_{2}.\)

이와 같이 설명이 되어있다.
결국 우리가 사용하는 것은 Cross Product의 Sign을 이용하여, p3의 위치가 p1과 p2가 이루는 직선의 좌측에 있나, 우측에 있나를 판별하는 것이다.

하지만 위의 글을 보면 “right-handed” cordinate system에서만 적용 된다 쓰여있다. 그럼으로, right-handed와 left-handed cordinate system에 대하여 구분을 해주어야 한다.

Left-handed, Right-handed Cordinate System

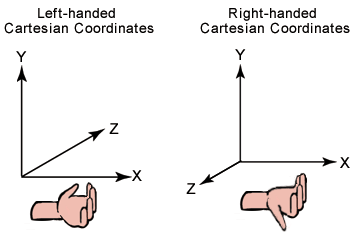left-hadned and Right-handed Cordinate System

해당 그림이 보여주는대로 Left-handed Cordiante System과 Right-handed Cordinate System과의 차이는 z축의 방향이 어디를 향하고 있는가로 나누어지게 된다. 그럼으로 CCW알고리즘의 결과를 해석하는 뱡향도 달라지게 된다.
Left-handed Cordinate System 기준으로 결과값이 음수라면, p1과 p2가 이루는 직선의 좌측에 p3가 있고, 결과값이 양수라면 p3가 직선의 우측에 있고, 결과값이 0 이면, p3가 직선 위에 있다.

Right-handed Cordinate System은 이와 반대로, 결과값이 음수라면 p3가 직선의 우측에 있고, 결과값이 양수라면 p3가 직선의 좌측에 있고, 결과값이 0 이면, p3가 직선 위에 있다.

결론

\(p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})\) and \(p_{3}=(x_{3},y_{3})\).
\(P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})\)

p1과 p2가 이루는 직선에 대한 p3의 위치

Cordinate System	P < 0	P = 0	P > 0
Left-Handed	좌측(반시계 방향)	직선 위	우측(시계 방향)
Right-Handed	우측(시계 방향)	직선 위	좌측(반시계 방향)